2D Physics Simulation

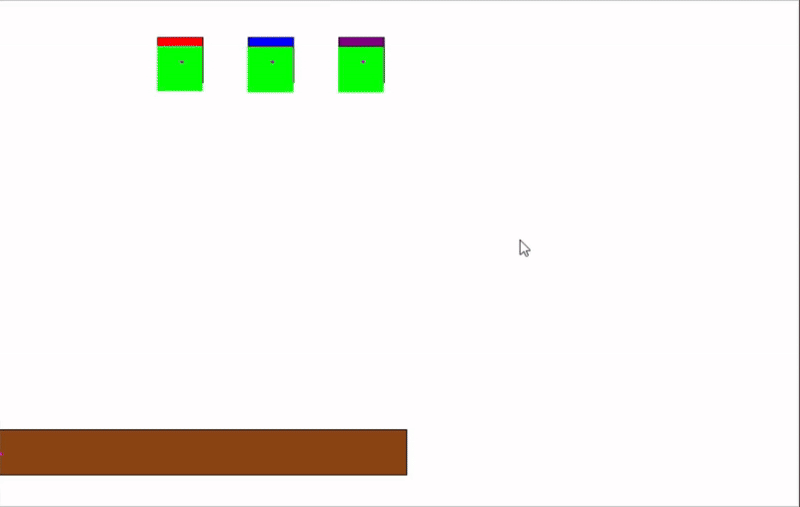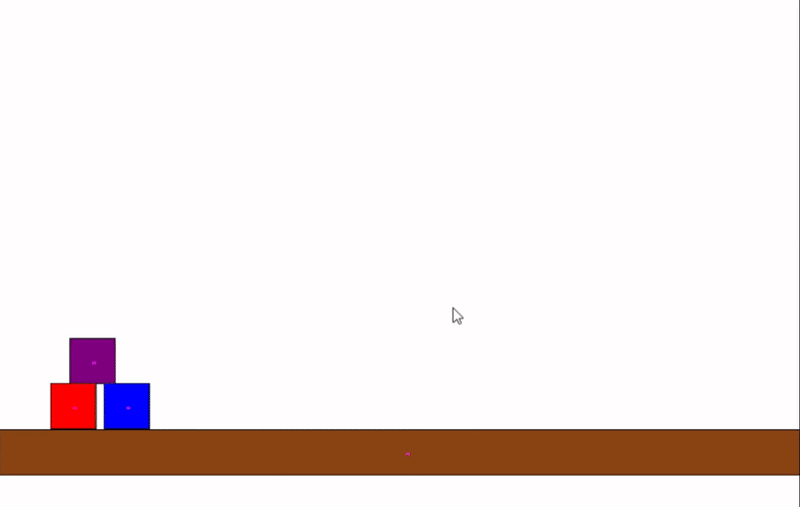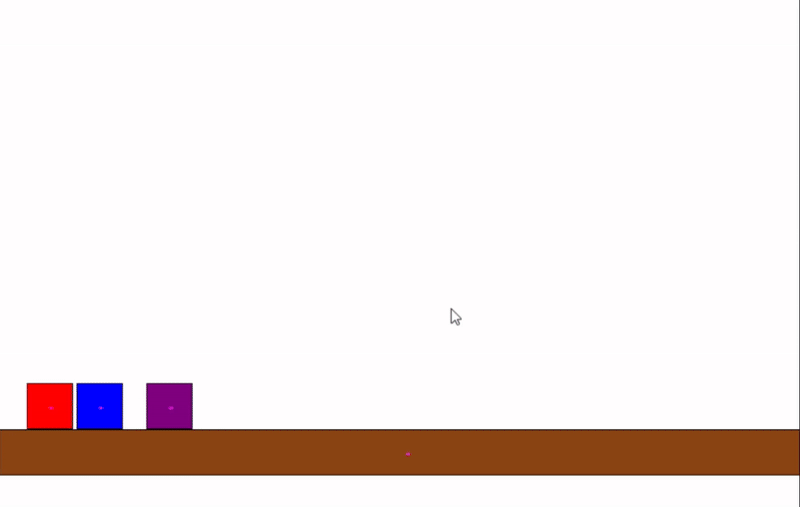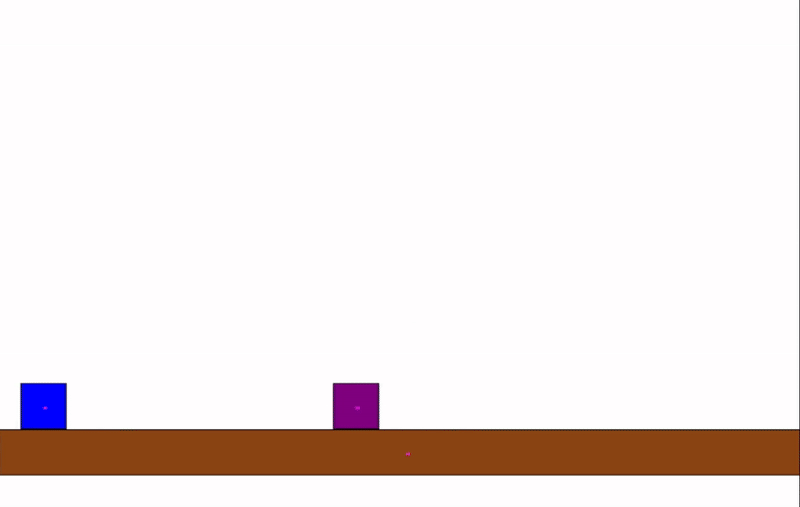
Project Overview

This project is a basic 2D physics simulation written in Java. It features a custom physics engine with real-time collision detection and response between simple shapes, such as circles and rectangles. The simulation demonstrates fundamental concepts in physics and computational geometry, and visualizes how objects interact in a 2D environment.

The main goal of this project is to deepen the understanding of game physics and the implementation of efficient collision detection algorithms, which are essential for realistic interactions in games and simulations. The codebase is modular and clearly documented, making it an excellent learning resource for anyone interested in game development or physics programming.

Collision Detection in Practice

The engine checks for collisions between objects every frame. For circles, it uses the distance between centers; for rectangles, it uses axis-aligned bounding box (AABB) checks. When a collision is detected, the engine calculates the overlap and applies a response so the objects bounce off each other realistically.

This approach allows for fast and accurate detection, making it suitable for real-time applications like games or interactive demos.

Theory: How Collision Detection Works

AABB Collision

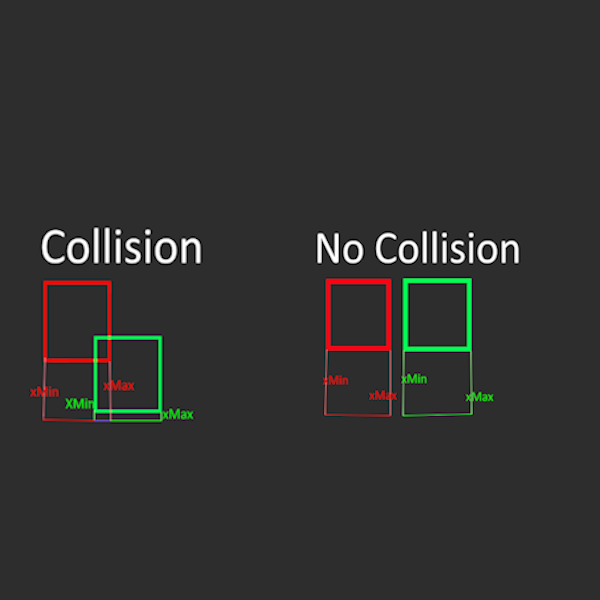
Rectangle (AABB) vs. Rectangle: Two rectangles collide if their projections on both the X and Y axes overlap. This is known as Axis-Aligned Bounding Box (AABB) collision detection. AABB is very fast because it only requires comparing the min and max values of the rectangles on each axis. It works best for rectangles that are not rotated.

PseudoCode ⮞

collision: just compare min/max on X and Y
  boolean aabbCollide(Rect a, Rect b) {
    return a.x < b.x + b.width &&
        a.x + a.width > b.x &&
        a.y < b.y + b.height &&
        a.y + a.height > b.y;
  }
            

SAT Collision

SAT (Separating Axis Theorem): SAT is a more advanced algorithm that can detect collisions between any convex polygons, including rotated rectangles. It works by projecting the shapes onto potential separating axes and checking for overlaps. If a separating axis is found where the projections do not overlap, the shapes are not colliding. SAT is more flexible but also more computationally expensive than AABB.

Pseudocode ⮞

collision:
  boolean satCollide(Polygon polyA, Polygon polyB) {
    for (Vector axis : getAxes(polyA, polyB)) {
      Projection projA = project(polyA, axis);
      Projection projB = project(polyB, axis);
      if (!projA.overlaps(projB)) {
        return false; // Found a separating axis
      }
    }
    return true; // No separating axis, collision!
  }
            

Circle Collision

Circle vs. Circle: Two circles collide if the distance between their centers is less than the sum of their radii. This is calculated using the Pythagorean theorem.

How SAT and AABB Are Used Together

In this project, SAT (Separating Axis Theorem) is used for accurate collision detection between all shapes, including rotated rectangles and polygons. SAT determines if two objects will collide by checking for a separating axis between them.

Once a collision is detected with SAT, AABB (Axis-Aligned Bounding Box) logic is used to calculate the collision resolution, specifically, to determine the separation axis and penetration depth for resolving overlaps. This approach combines the accuracy of SAT for detection with the simplicity and efficiency of AABB for resolving collisions, especially for axis-aligned objects.

This method ensures that the simulation is both robust (able to handle complex shapes) and efficient (fast resolution for common cases), matching the real implementation in the code.

Code Examples

public boolean overlapsOnAxis(Collider other, Vector2 axis) {
    float[] projA = this.projectOntoAxis(axis);
    float[] projB = other.projectOntoAxis(axis);
    return !(projA[1] < projB[0] || projB[1] < projA[0]);
}

public float[] projectOntoAxis(Vector2 axis) {
    ArrayList worldPoints = getWorldPoints();
    if (worldPoints.isEmpty()) {
        return new float[]{0f, 0f};
    }
    
    float min = (float) worldPoints.get(0).dot(axis);
    float max = min;
    
    for (int i = 1; i < worldPoints.size(); i++) {
        float projection = (float) worldPoints.get(i).dot(axis);
        min = Math.min(min, projection);
        max = Math.max(max, projection);
    }
    
    return new float[]{min, max};
}
                

public boolean overlapsWithCircle(CircleCollider other) {
    Vector2 thisCenter = this.getObject().futureTransform.position;
    Vector2 otherCenter = other.getObject().futureTransform.position;
    float distance = (float) thisCenter.distance(otherCenter);
    return distance < (this.radius + other.radius);
}
                

public boolean intersects(Collider other) {
        if (other == null) {
            return false;
        }
        
        ArrayList axesA = this.getAxes();
        ArrayList axesB = other.getAxes();
        
        if (axesA.isEmpty() || axesB.isEmpty()) {
            return false;
        }
        
        for (Vector2 axis : axesA) {
            if (axis.magnitude() < 0.001f) continue;
            if (!this.overlapsOnAxis(other, axis)) {
                return false;
            }
        }
        
        for (Vector2 axis : axesB) {
            if (axis.magnitude() < 0.001f) continue;
            if (!this.overlapsOnAxis(other, axis)) {
                return false;
            }
        }
        
        return true;
    }